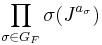Stickelberger's theorem

In mathematics, Stickelberger's theorem is a result of algebraic number theory, which gives some information about the Galois module structure of class groups of cyclotomic fields. A special case was first proven by Ernst Kummer (1847) while the general result is due to Ludwig Stickelberger (1890).^[1]

1 The Stickelberger element and the Stickelberger ideal
- 1.1 Examples
2 Statement of the theorem
3 See also
4 Notes
5 References
6 External links

The Stickelberger element and the Stickelberger ideal

Let K_m denote the mth cyclotomic field, i.e. the extension of the rational numbers obtained by adjoining the mth roots of unity to Q (where m ≥ 2 is an integer). It is a Galois extension of Q with Galois group G_m isomorphic to the multiplicative group of integers modulo m (Z/mZ)^×. The Stickelberger element (of level m or of K_m) is an element in the group ring Q[G_m] and the Stickelberger ideal (of level m or of K_m) is an ideal in the group ring Z[G_m]. They are defined as follows. Let ζ_m denote a primitive mth root of unity. The isomorphism from (Z/mZ)^× to G_m is given by sending a to σ_a defined by the relation

σ_a(ζ) = ζ a
m .

The Stickelberger element of level m is defined as

$\theta(K_m)=\frac{1}{m}\underset{(a,m)=1}{\sum_{a=1}^m}a\cdot\sigma_a^{-1}\in\mathbf{Q}[G_m].$

The Stickelberger ideal of level m, denoted I(K_m), is the set of integral multiples of θ(K_m) which have integral coefficients, i.e.

$I(K_m)=\theta(K_m)\mathbf{Z}[G_m]\cap\mathbf{Z}[G_m].$

More generally, if F be any abelian number field whose Galois group over Q is denoted G_F, then the Stickelberger element of F and the Stickelberger ideal of F can be defined. By the Kronecker–Weber theorem there is an integer m such that F is contained in K_m. Fix the least such m (this is the (finite part of the) conductor of F over Q). There is a natural group homomorphism G_m → G_F given by restriction, i.e. if σ ∈ G_m, its image in G_F is its restriction to F denoted res_mσ. The Stickelberger element of F is then defined as

$\theta(F)=\frac{1}{m}\underset{(a,m)=1}{\sum_{a=1}^m}a\cdot\mathrm{res}_m\sigma_a^{-1}\in\mathbf{Q}[G_F].$

The Stickelberger ideal of F, denoted I(F), is defined as in the case of K_m, i.e.

$I(F)=\theta(F)\mathbf{Z}[G_F]\cap\mathbf{Z}[G_F].$

In the special case where F = K_m, the Stickelberger ideal I(K_m) is generated by (a − σ_a)θ(K_m) as a varies over Z/mZ. This not true for general F.^[2]

Examples

If F is a totally real field of conductor m, then^[3]

$\theta(F)=\frac{\phi(m)}{2[F:\mathbf{Q}]}\sum_{\sigma\in G_F}\sigma,$

where φ is the Euler totient function and [F : Q] is the degree of F over Q.

Statement of the theorem

Stickelberger's Theorem^[4]

Let F be an abelian number field. Then, the Stickelberger ideal of F annihilates the class group of F.

Note that θ(F) itself need not be an annihilator, but any multiple of it in Z[G_F] is.

Explicitly, the theorem is saying that if α ∈ Z[G_F] is such that

$\alpha\theta(F)=\sum_{\sigma\in G_F}a_\sigma\sigma\in\mathbf{Z}[G_F]$

and if J is any fractional ideal of F, then

$\prod_{\sigma\in G_F}\sigma(J^{a_\sigma})$

is a principal ideal.

Notes

^ Washington 1997, Notes to chapter 6
^ Washington 1997, Lemma 6.9 and the comments following it
^ Washington 1997, §6.2
^ Washington 1997, Theorem 6.10

References

Boas Erez, Darstellungen von Gruppen in der Algebraischen Zahlentheorie: eine Einführung
Kummer, Ernst (1847), "Über die Zerlegung der aus Wurzeln der Einheit gebildeten complexen Zahlen in ihre Primfactoren", Journal für die Reine und Angewandte Mathematik 35: 327–367
Stickelberger, Ludwig (1890), "Ueber eine Verallgemeinerung der Kreistheilung", Mathematische Annalen 37 (3): 321–367, JFM 22.0100.01, MR 1510649, http://gdz.sub.uni-goettingen.de/no_cache/dms/load/img/?IDDOC=27547
Washington, Lawrence (1997), Introduction to Cyclotomic Fields, Graduate Texts in Mathematics, 83 (2 ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-94762-4, MR 1421575

External links

PlanetMath page